√ Diagram Venn : Pengertian, Cara Membuat, Macam Dan Pola Soalnya Lengkap
Mengenal Diagram Venn Secara Lengkap
Daftar Isi :
Diagram Venn – Diagram venn diperkenalkan oleh spesialis matematika asal Inggris pada tahun 1834 – 1923. Mengapa disebut dengan nama diagram venn? Karena penemunya berjulukan Jhon Venn, yang dimana venn tersebut diambil dari nama belakang penemu diagram tersebut. definisi dari diagram venn yaitu gambar himpunan, yang menyatakan beberapa himpunan dan campuran diantara beberapa himpunan dalam semesta pembicaraan tertentu.

Hal-Hal Yang Harus Diperhatikan Dalam Membuat Diagram Venn
- Membuat persegi panjang atau juga persegi terlebih dahulu.
- Himpunan semesta digambarkan dengan gambar persegi panjang, dengan lambang S yang dimana ditulis di sudut kiri atas di dalam gambar persegi panjang tersebut. himpunan S yaitu jenis himpunan yang memuat seluruh anggota himpunan, yang dibicarakan.
- Setiap himpunan lainnya yang dibicarakan dalam gambar dengan bundar atau kurva tertutup, kecuali yang tidak termasuk ke dalam himpunan yang lain yang dituliskan di luar lingkaran.
- Setiap anggota ditunjukkan dengan tanda noktah atau titik dan anggota himpunan ditulis di samping noktah tersebut.
Contoh diagram venn menyerupai berikut :
S={1,2,3,4,5,6,7,8,9}
A={1,3,4,2,5}
B={2,5,7,6}
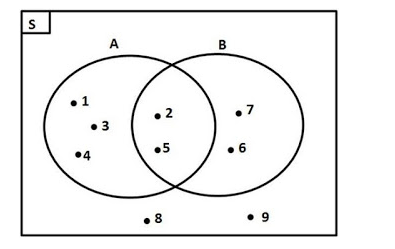
Hubungan Diantara Dua Himpunan
1. Himpunan yang berpotongan
Himpunan A dan B akan saling berpotongan apabila ada anggota himpunan A dan B yang sama. Himpunan A juga berpotongan dengan himpunan B dan sanggup ditulis dengan . Himpunan yang berpotongan tersebut sanggup dinyatakan ke dalam diagram venn menyerupai berikut :
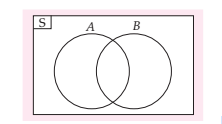
2. Himpunan saling lepas
Himpunan A dan B akan saling lepas kalau tak ada anggota himpunan A dan B yang sama. Himpunan A saling lepas dengan himpunan B dan ditulis dengan . Himpunan saling lepas dari himpunan A dan B dinyatakan dengan diagram venn, menyerupai pada gambar berikut ini :
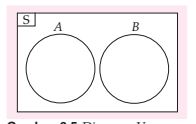
3. Himpunan bagian
Himpunan A sanggup disebut himpunan bab dari himpunan B kalau seluruh anggota himpunan A yaitu anggota dari himpunan B. himpunan A yaitu bab dari himpunan B dan sanggup dinyatakan dengan diagram venn menyerupai pada gambar berikut :
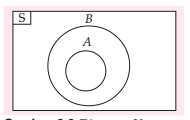
4. Himpunan yang sama
Himpunan A dan B sanggup disebut dengan himpunan yang sama apabila setiap anggota A yaitu anggota B, dan setiap anggota B yaitu anggota A. contohnya A = {1, 2, 3} dan B = {3, 2, 1} bisa disebut sebagai himpunan A yang sama dan himpunan B sanggup ditulis dengan A = B. dengan diagram venn yang dinyatakan menyerupai pada gambar berikut :
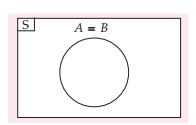
5. Himpunan yang ekuivalen
Dua himpunan sanggup disebut ekuivallen apabila banyaknya anggota dari kedua himpunan itu sama. Contohnya A = {a, b, c, d}; B = {1, 2, 3, 4} A dan B disebut dengan himpunan yang ekuivalen. Himpunan A ekuivalen dengan himpunan B kalau n(A) = n(B).
Di dalam himpunan terdapat beberapa istilah menyerupai irisan, gabungan, selisih dan juga komplemen.
1. Irisan himpunan
Irisan dari kedua himpunan A dan B yaitu jenis himpunan yang beberapa anggotanya berada di himpunan A dan B. yang sanggup disebut dengan himpunan yang anggotanya berada di kedua himpunan tersebut.
Contohnya : A = {a, b, c, d, e} dan B = {b, c, f, g, h}
Di kedua himpunan tersebut terdapat dua anggota yang sama yaitu B dan C. oleh alasannya yaitu itu sanggup dikatakan bahwa irisan pada himpunan A dan B yaitu B dan C yang ditulis dengan A ∩B = {b, c}.
A∩B dibaca dengan himpunan A irisan himpunan B. diagram venn A∩B sanggup dinyatakan dengan gambar berikut ini :
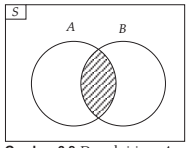
2. Gabungan himpunan
Adalah suatu himpunan yang beberapa anggotanya yaitu anggota pada himpunan A dan B atau bab dari anggota keduanya.
Contohnya A = {1, 2, 3, 4} dan B = {4, 5, 6, 7}
Gabungan dari kedua himpunan A dan B yaitu {1, 2, 3, 4, 5, 6, 7} atau sanggup juga ditulis dengan A ᴗB = {1, 2, 3, 4, 5, 6, 7}
AᴗB dibaca dengan himpunan A campuran himpunan B. yang ditunjukkan ke dalam gambar berikut :

4. Komplemen
Komplemen dari himpunan A yaitu himpunan yang anggotanya bukan anggota A.
Contohnya S = {0, 1, 2, 3, 4, 5, 6, 7}
A = {2, 3, 4, 5}
Komplemen dari himpunan A yaitu {0, 1, 6, 7}. Komponen dari himpunan A tersebut dinotasikan atau ditulis dengan A’ yang dibaca A komplemen, atau suplemen dari A. suplemen A juga sanggup dinyatakan dengan diagram venn. Yang sanggup dilihat pada gambar berikut :
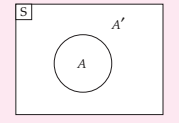
Contoh Soal
Perhatikan diagram Venn Di bawah ini
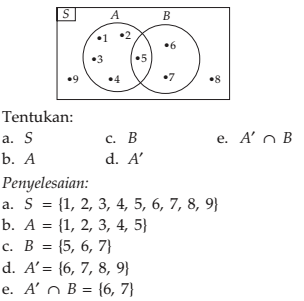
Demikian bahan pembahasan perihal diagram venn yang lengkap. Semoga sanggup menambah wawasan dan pengetahuan anda.
Baca Juga :
Notasi Sigma : Pengertian, Materi, Sifat, Rumus Dan Contoh Soalnya Lengkap
Materi Relasi Dan Fungsi : Fungsi Komposisi Dan Fungsi Invers Lengkap
Sumber aciknadzirah.blogspot.com